ترجمه تخصصی متون توپولوژی

توپولوژی^[۱] شاخه‌ای از ریاضیات است که به بررسی فضاهای توپولوژیکی و خواص بنیادی فضا از جمله همبندی می‌پردازد. توپولوژی یکی از شاخه‌های نسبتاً جوان ریاضیات است.

نام این رشته از واژه‌های یونانی توپو (τόπος) به‌معنی مکان و (Logos) به‌معنای شناخت گرفته شده‌ است. بنابراین، توپولوژی یعنی مکان‌شناسی.

فرهنگستان زبان و ادب فارسی برای توپولوژی واژه‌ای معادل پیشنهاد نکرده‌ و همان توپولوژی را در نظر گرفته‌ است.

این مبحث نخستین‌بار توسط آنری پوانکاره (۱۹۱۲-۱۸۵۴) و در مقاله‌ای با نام «آنالیز مکان» (Analysis Situs) به‌صورت مجموعه‌ای از روش‌ها و مسایل، دسته‌بندی شد. این مبحث در ادامه پیشرفت‌هایی بنیادین داشت و در شکل دادن به ریاضیات قرن بیستم و امروز، نقشی اساسی بازی کرد.

هنگام صحبت از توپولوژی، معمولاً اشیایی مانند نوار موبیوس، بطری کلاین، گره‌ها و حلقه‌ها نخستین چیزهایی هستند که به ذهن می‌آیند. برخی نیز با عبارتی طنزآمیز توپولوژیست‌ها را توصیف می‌کنند؛ آنها می‌گویند توپولوژیست کسی است که فرقی میان فنجان قهوه و پیراشکی نمی‌بیند!

در دهه ۱۶۷۰ میلادی، گتفرید ویلهلم لایب‌نیتس (۱۷۱۶-۱۶۴۶)، در نامه‌ای به کریستین هویگنس (۱۶۲۹-۱۶۹۵)، به تشریح مفهومی پرداخت که بعدها به مهم‌ترین هدف در مطالعه توپولوژی تبدیل شد:

من معتقدم ما به یک آنالیز دیگری هم نیاز داریم که کاملاً هندسی یا خطی باشد، به‌گونه‌ای که با مکان مستقیماً همان رفتاری را داشته باشد که جبر با مفهوم بزرگی دارد.

لایب‌نیتس رویای حساب دیفرانسیل و انتگرال اشکالی را در سر می‌پروراند که در آن فرد می‌تواند به‌سادگی اعداد و اشکال را با هم ترکیب کند، مانند چندجمله‌ای‌ها، روی آنها عمل انجام دهد و به نتایج جدید و متقن هندسی دست پیدا کند. این دانش مکان، همان است که پوانکاره آن را «آنالیز مکان» نامید. کسی نمی‌داند که لایب‌نیتس دقیقاً چه در سر داشت؛ اما پیداست که لئونارد اویلر (۱۷۰۱-۱۷۸۳) نخستین مشارکت‌ها را در این شاخهٔ جوان--که وی آن را هندسه مکان می‌نامید--از خود ارائه داد. راه‌حل او برای مسئلهٔ پل‌های کنیگسبرگ و فرمول مشهور اویلر، یعنی 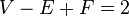$V-E+F=2$ (که در آن $V$ تعداد رأس، $E$ تعداد یال و $F$ تعداد وجوه چندوجهی است)، نتایجی بودند که به موقعیت‌های نسبی اشکال هندسی--و نه بزرگی آنها--بستگی داشتند.

در سده نوزدهم، کارل فردریک گاوس (۱۷۷۷-۱۸۵۵)، هنگامی که گره‌ها و حلقه‌ها را به‌عنوان تعمیمی از مدارهای سیارات مطالعه می‌کرد، به هندسه مکان علاقه‌مند شد. او با نام‌گذاری اشکال گره‌ها و حلقه‌ها، یک دستگاه مقدماتی به‌وجود آورد که با روش ترکیبیاتی، گره‌های معینی را از یکدیگر مجزا می‌ساخت. برنهارد ریمان (۱۸۲۶-۱۸۶۶) نیز از روش‌های دانش نوپای آنالیز مکان، به‌عنوان ابزاری بنیادین برای مطالعه توابع مختلط بهره جست.

در طی سده نوزدهم، آنالیز به‌عنوان دانشی ژرف و در عین حال ظریف پیشرفت پیدا می‌کرد. با آغاز از کارهای ژرژ کانتور (۱۸۴۵-۱۹۱۸)، ایده‌هایی از جمله پیوستگی توابع و هم‌گرایی دنباله‌ها، به‌گونه‌ای فزاینده و در موقعیت‌های کلی بررسی می‌شدند تا این که در سده بیستم، و در سال ۱۹۱۴، فلیکس هاوسدورف (۱۸۶۹-۱۹۴۲) ایده کلی فضای توپولوژیکی را مطرح کرد.

مفهوم بنیادین در توپولوژی، اندیشه پیوستگی است و این مفهوم برای نگاشت‌های میان دو مجموعه که مجهز به مفهومی از «نزدیک بودن» باشند تعریف می‌شود (یعنی همان فضاهای توپولوژیکی) و البته این نزدیک بودن، تحت نگاشت‌های پیوسته حفظ می‌شود. بدین ترتیب، می‌توان گفت توپولوژی نوعی هندسه‌ است که در آن خواص مهم یک شکل، آنهایی درنظر گرفته می‌شوند که تحت حرکت‌های پیوسته (همئومورفیسم‌ها) حفظ گردند. از این دیدگاه، توپولوژی را می‌توان به‌عنوان هندسه‌ی صفحاتی لاستیک‌گونه تعریف کرد.

توپولوژی یکی از زمینه‌های مهم ریاضیات است که از پیشرفت مفاهیمی از هندسی و نظریه مجموعه‌ها مانند فضا، بعد، اشکال، تبدیلات و... بوجود آمده‌ است. از جنبه تاریخی توپولوژی در سال ۱۸۴۷ از سوی لیستنگ، یکی از شاگردان گاوس، معرفی شد. نام دیگری که در آغاز بسط توپولوژی به این موضوع اطلاق می‌شد، آنالیز موقعیت (Analysis Situs) بود.

توپولوژی دارای زیرشاخه‌های زیادی است. بنیادی‌ترین و قدیمی‌ترین زیرشاخه، توپولوژی نقطه-مجموعه‌ است که بنیادهای توپولوژی بر آن بنا شده‌ است و به مطالعه در زمینه‌های فشردگی، پیوستگی و هم‌بندی می‌پردازد. توپولوژی جبری نیز یکی دیگر از زیرشاخه‌های توپولوژی است که سعی در محاسبه درجه هم‌بندی دارد. همچنین زیرشاخه‌هایی مانند توپولوژی هندسی، توپولوژی گراف و توپولوژی ابعاد پایین نیز وجود دارند.

توپولوژی مطالعه ریاضیاتی روی خصوصیاتی است که در طی تغییر شکلها، ضربه خوردن‌ها و کشیده شدن اشیاء، به طور ثابت حفظ می‌شوند (البته عمل پاره کردن مجاز نمی‌باشد). یک دایره به لحاظ توپولوژیکی هم‌ارز با یک بیضی می‌باشد که می‌تواند در داخل آن با کشیده شدن تغییر شکل یابد و یک کره با یک سطح بیضی‌وار هم‌ارز است (یعنی یک منحنی بسته تک بعدی و بدون هیچ محل تقاطع که می‌تواند در فضای دو بعدی جای گیرد)، مجموعه تمام وضعیتهای ممکن برای عقربه‌های ساعت‌شمار و دقیقه‌شمار با هم، به لحاظ توپولوژیکی با چنبره هم‌ارز است (یعنی یک سطح دوبعدی که می‌تواند در داخل فضای سه بعدی جای گیرد) و مجموعه تمام وضعیت‌های ممکن برای عقربه‌های ساعت‌شمار، دقیقه‌شمار و ثانیه‌شمار با هم، به لحاظ توپولوژی با یک شیء سه بعدی هم‌ارز می‌باشد.

توپولوژی با منحنی‌ها، سطوح و سایر اشیاء در صفحه و فضای سه بعدی مطرح گردید. یکی از ایده‌های اصلی در توپولوژی این است که اشیاء فضایی مثل دایره‌ها و کره‌ها در نوع خود می‌توانند به عنوان اشیاء محسوب شوند و علم اشیاء ارتباطی با چگونگی نمایش یافتن یا جای گرفتن آنها در فضا ندارد.

توپولوژی با مطالعه مواردی چون اشیاء فضایی از قبیل منحنی‌ها، سطوح، فضایی که ما آن را جهان می‌نامیم، پیوستار فضا زمان با نسبیت عمومی، فراکتال‌ها، گره‌ها، چند شکلی‌ها (اشیایی هستند که برخی خصوصیات فضایی اصلی آن‌ها مشابه با جهان ما می‌باشد)، فضاهای مرحله‌ای که در فیزیک با آن‌ها مواجه می‌شویم (مثل فضای وضعیت‌های قرار گرفتن عقربه‌ها در ساعت)، گروه‌های متقارن همچون مجموعه شیوه‌های چرخاندن یک رأس و غیره در ارتباط است.

توپولوژی برای جدا سازی اتصال ذاتی اشیاء و در عین حال کنار گذاشتن ساختار جزء به جزء آنها قابل استفاده می‌باشد. اشیاء توپولوژیکی اغلب به صورت رسمی به عنوان فضاهای توپولوژیکی تعریف می‌شوند. اگر دو شیء دارای خصوصیات توپولوژیکی مشابه باشند، گفته می‌شود که آن‌ها هم ریخت هستند. البته اگر دقیق تر بگوییم، خصوصیاتی که با کشیدن یا کج کردن یک شیء تخریب نمی‌شوند، در واقع خصوصیاتی هستند که به واسطه همسانگری حفظ می‌شوند نه به واسطهٔ هم ریختی؛ همسانگری با کج کردن اشیاء دیگر در ارتباط است در حالیکه همریختی، خصیصه ذاتی است.

حدود سال ۱۹۰۰، پوانکاره معیاری از توپولوژی را تحت عنوان هوموتوپی (Homotopy) طراحی کرد. به طور خاص دو شیء ریاضیاتی زمانی هوموتوپیک خوانده می‌شوند که یکی از آنها بتواند به طور پیوسته به شکلی مشابه شکل دیگری تغییر یابد.

توپولوژِی با مطالعاتی که در زمینه پرسش‌هایی که در هندسه مطرح بود، آغاز شد. مسئله ۷ پل کانیگزبرگ اویلر جز اولین نتایج توپولوژیک بود. نمونه رابطه توپولوژیکی، فرمول اویلر است در مورد چندوجهی‌ها که تعداد رئوس (v) منهای تعداد خطوط یا لبه‌ها (e) باضافه تعداد سطوح (f) همیشه برابر است با ۲ است. (v – e + f = ۲)

فرمول اویلر در سال ۱۷۵۲ منتشر شد ولی ۶۳ سال بعد در سال ۱۸۱۳ ریاضیدان سویسی بنام لیولیر اثبات کرد که فرمول اویلر برای چندوجهی‌های سوراخدار صحیح نیست و فرمول کامل چنین است: v – e + f = ۲g، که g تعداد سوراخ‌ها است.

۵۲ سال بعد از لیولیر، در سال ۱۸۶۵، موبیوس نوار خود را معرفی کرد که فقط یک رویه دارد و از نواری بدست می‌آید که قبل از چسباندن دو سرش به یکدیگر، یک سر را ۱۸۰درجه بچرخانیم و بعد بچسبانیم. ۱۷ سال بعد در سال ۱۸۸۲ ریاضیدان آلمانی فلیکس کلاین بطری معروف به «بطری کلاین» را معرفی کرد که درون و برون آن از هم متمایز نیستند و بعبارتی دیگر حجم آن صفر است. توپولوژی مدرن وابسته به ایدهٔ تئوری مجموعه‌های کانتر می‌باشد که در مهندس علاییخر قرن ۱۹ مطرح شد.

مجموعه X به همراه گردایه T از زیرمجموعه‌های X را یک فضای توپولوژیکی گویند هر گاه: مجموعه‌های تهی و X، عضو T باشند. اجتماع هر گردایه از مجموعه‌های عضو T در T قرار دارد. اشتراک هر دو مجموعه عضو T در T قرار دارد. مجموعه T را یک توپولوژی روی X می‌گوییم. همچنین اعضای T مجموعه‌های باز در X و متتم آنها مجموعه‌های بسته در X هستند. اعضای X را نقاط می‌نامیم. وی یک مجموعه مانند X توپولوژیهای متعددی می‌توان تعریف کرد (حداقل دو توپولوژی گسسته و ناگسسته را می‌توانیم روی X تعریف کنیم). حال فرض کنید T۱ و T۲ دو توپولوژی روی X هستند. اگر هر عضو T۱، عضوی از T۲ نیز باشد آنگاه می‌گوییم T۲ ظریفتر از T۱ است. در این صورت اثباتی که برای وجود یک مجموعه باز معین ارائه می‌دهیم در مورد توپولوژی ظریفتر هم برقرار است. توابع پیوسته: فرض می‌کنیم (X,T) و (Y,U) دو فضای توپولوژیک دلخواه باشند: تابع در نقطه x واقع در X را پیوسته گوییم، هرگاه به ازای هر مجموعه باز شامل f(x) مانند BY، مجموعه بازی مانند BX شامل x وجود داشته باشد به طوری که f[BX] زیر مجموعه BY باشد. مثال: R یک فضای توپولوژیکی است و مجموعه‌های باز در آن بازه‌های باز هستند. به طور کلی فضای اقلیدسی Rn یک فضای توپولوژیکی است و مجموعه‌های باز در آن گوی‌های باز هستند. چند قضیه توپولوژی: هر بازه بسته با طول متناهی در Rn فشرده‌است. و معکوس تصویر پیوسته یک فضای فشرده، فشرده‌است. قضیه تیخونوف: حاصلضرب فضاهای فشرده، یک فضای فشرده‌است. زیر مجموعه فشرده یک فضای هاسدورف، بسته‌است. هر فضای متری هاسدورف است. به همین ترتیب می‌گوییم تابع در مجموعهٔ A واقع در X پیوسته‌است رد صورتی که در تمام نقاط A پیوسته باشد. قضیه: تابع در X پیوسته‌است اگر و تنها اگر به ازای هر زیر مجموعه باز در Y مانند BY، مجموعه‌یf[BY] − ۱ زیر مجموعه باز X باشد. به طور خلاصه: فرض کنید X و Y دو فضای توپولوژیکی هستند. یک تابع بین X و Y را پیوسته می‌گوییم اگر تصویر معکوس هر مجموعه باز در X یک مجموعه باز در Y باشد. در واقع نشان می‌دهیم که هیچ شکستگی یا انفصال در تابع وجود ندارد.

یک فضای توپولوژیک، زوج مرتبی مانند $(X,T)$ است که در آن $X$ یک مجموعه، و ${T}$ نیز گردایه‌ای از زیرمجموعه‌های $X$ است، به‌گونه‌ای که اصول موضوع زیر ارضا شوند:

گردایهٔ $\mathcal{T}$ ، توپولوژی تعریف شده روی $X$ نام دارد. اگر توپولوژی تعریف شده روی $X$ مشخص باشد، فضای توپولوژیکی $(X, \mathcal{T})$ ، به‌طور ساده‌شدهٔ $X$ نوشته و به آن فضای $X$ گفته می‌شود. هم‌چنین، اعضای $\mathcal{T}$ ، مجموعه‌های باز در $X$ و متمم آنها، مجموعه‌های بسته در $X$ نام دارند. اگر $X$ یک فضای توپولوژیکی باشد، به اعضای آن نقطه گفته می‌شود. اگر $x$ نقطه‌ای از یک مجموعهٔ باز مانند $U$ باشد، به $U$ ، «یک همسایگی از $x$ » نیز گفته می‌شود.

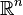روی $\mathbb{R}$ توپولوژی‌های گوناگونی می‌توان تعریف کرد؛ اگر مجموعه‌های باز را همان بازه‌های باز درنظر بگیریم، در این‌صورت به توپولوژی به‌دست آمده، توپولوژی استاندارد روی $\mathbb{R}$ گفته می‌شود. با تعمیم این ایده، مجموعه‌های باز در توپولوژی معمولی روی فضای اقلیدسی $\mathbb{R}^{n}$ ، گوی‌های باز هستند.

روی یک مجموعه مانند $X$ توپولوژی‌های متعددی می‌توان تعریف کرد--دست‌کم دو توپولوژی گسسته و ناگسسته. در توپولوژی گسسته، هر زیرمجموعه از $X$ ، یک مجموعه باز درنظر گرفته می‌شود و در توپولوژی ناگسسته یا بی‌مایه، تنها مجموعه‌های باز، مجموعهٔ $X$ و تهی هستند.

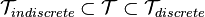برای هر توپولوژی $\mathcal{T}$ تعریف شده روی $X$ داریم $\mathcal{T}_{indiscrete} \subset \mathcal{T} \subset \mathcal{T}_{discrete}$ . پس درشت‌ترین توپولوژی که روی یک مجموعه می‌توان تعریف کرد، توپولوژی ناگسسته یا بی‌مایه، و ظریف‌ترین توپولوژی قابل تعریف روی یک مجموعه، توپولوژی گسسته‌است.

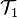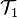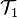حال فرض کنید $\mathcal{T}_{1}$ و $\mathcal{T}_{2}$ دو توپولوژی روی $X$ باشند. اگر هر عضو $\mathcal{T}_{1}$ ، عضوی از $\mathcal{T}_{2}$ نیز باشد، آن‌گاه گفته می‌شود $\mathcal{T}_{2}$ ظریف‌تر از $\mathcal{T}_{1}$ است. در این صورت اثباتی که برای وجود یک مجموعهٔ باز معین ارائه داده می‌شود، در مورد توپولوژی ظریف‌تر هم برقرار است.

تئوری گره‌ها، شاخه‌ای از توپولوژی است که در زیست‌شناسی برای مطالعه‌ی اثرات آنزیم‌ها روی دی.ان.ای به کار می‌رود. آنزیم‌هایی که دی.ان.ای ها را برش ‌می‌دهند،چرخش می‌دهند و دوباره به هم متصل می‌کنند، گره‌هایی با اثرات قابل مشاهده مانند الکتروفورز آهسته تر ایجاد می‌کنند. همچنین توپولوژی در زیست‌شناسی تکاملی برای بیان‌کردن رابطه‌ی بین فنوتیپ و ژنوتیپ به کار می‌رود. اشکال فونوتیپی که کاملا متفاوت به نظر می‌رسند، می‌توانند تنها به وسیله‌ی چند جهش وابسته به اینکه چگونه ژنتیک نقشه را عوض می‌کند، جدا شوند.

تحلیل داده توپولوٰیکی از تکنیک‌های توپولوژی جبری استفاده کرده تا ساختار انبوه یک مجموعه را محاسبه کند. روش اصلی‌ای که تحلیل داده توپولوژیکی از آن استفاده می‌کند، عبارت است از:

در فیزیک، توپولوژی در چندین شاخه مانند نظریه میدان‌های کوانتومی و کیهان‌شناسی کاربرد دارد. یک نظریه میدان‌های کوانتومی توپولوژیکی (یا نظریه میدان‌های توپولوژیکی)، یک نظریه میدان‌های کوانتومی است که ویژگی‌های توپولوژيکی را محاسبه می‌کند. گرچه این شاخه توسط فیزیکدان‌ها به وجود آمده است اما از علاقه‌مندی‌های ریاضی‌دانان نیز هست. نظریه گره‌ها و نظریه چهار برابری در توپولوژي جبری و نظریه فضاهای مدول در هندسه‌ جبری. سیمون دونالسون، وان جونز، ادوارد ویتن . ماکسیم کانسویچ برای کار روی نظریه میدان‌های توپولوژیکی، مدال فیلدز برده‌اند. در کیهان‌شناسی، توپولوژی برای توصیف شکل کلی کیهان به کار می‌رود. این شاخه توپولوژی فضازمان نام دارد.

حالت‌های مختلف ممکن برای یک روبوت می‌تواند به وسیله‌ی خمینه‌هایی که فضای پیکربندی نام دارد، توصیف شود. در مبحث برنامه‌ریزی حرکت، یک مسیر بین دو نقطه را در فضای پیکربندی پیدا می کند. این مسیرها حرکت مفاصل یک ربات و دیگر قسمت‌های مطلوب را ارائه می‌دهند.

‎

ریاضیات محض • ریاضیات کاربردی • حساب • منطق ریاضی • نظریه مجموعه‌ها • نظریه رده‌ها • جبر (مقدماتی – خطی – مجرد) • نظریه اعداد • آنالیز ریاضی • هندسه • مثلثات • توپولوژی • نظریه سامانه‌های پویا • ترکیبیات • نظریه بازی‌ها • نظریه اطلاعات • بهینه‌سازی • نظریه محاسبات • احتمالات • آمار • فیزیک ریاضی

الگو:Link GA

سفارش ترجمه متون تخصصی توپولوژی

جهت سفارش ترجمه با سرپرست تیم مترجم سایت ما تماس بگیرید.

Telegram: @ChiefTranslator